人间如隙时光如驹
又活一岁
# 贝塞尔曲线 (opens new window)
我们通常用线条来绘制 2D 图形,大致分为两种线条:直线和曲线。不论我们动手还是用计算机,都能很容易地画出第一种线条。只要给计算机起点和终点,直线就画出来了。 然而,绘制曲线却是个大问题。我们必须准确的描述一个曲线给到计算机,否则我们用笔很容易画出来的弯钩,弧线,很难在电脑上来复现。
计算机画线是需要一个函数来进行定义,直线是很好定义的 p(t) = p0 + (1-t)(p1 - p0),但是对于弧线来说有非常多种的函数定义。这里就要介绍到今天的主角,贝塞尔曲线了
贝塞尔曲线于 1962 年,由法国工程师皮埃尔·贝兹(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计,由于它的一些特殊性质,使得在计算机中广泛应用这种曲线来进行定义弧线
# 一次(线性)贝塞尔曲线
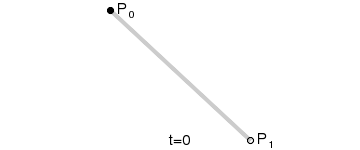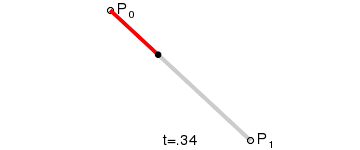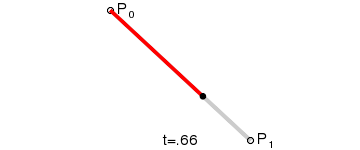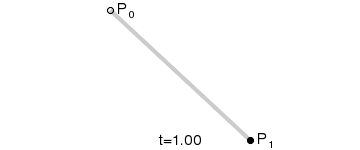
给定点 P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:
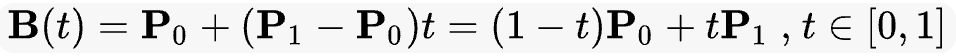
且其等同于线性插值 (opens new window)。
# 二次方贝塞尔曲线
二次方贝塞尔曲线的路径由给定点 P0、P1、P2 的函数 B(t):
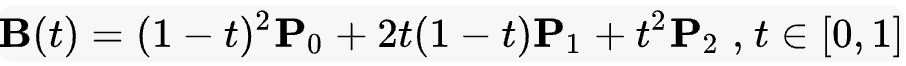
示意图
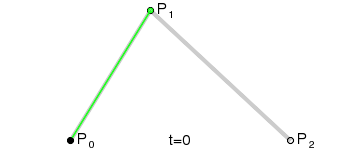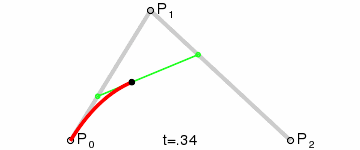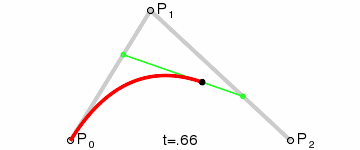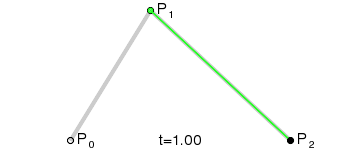
# 三次方贝塞尔曲线
P0、P1、P2、P3 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于 P0 走向 P1,并从 P2 的方向来到 P3。一般不会经过 P1 或 P2;这两个点只是在那里提供方向信息。P0 和 P1 之间的间距,决定了曲线在转而趋进 P2 之前,走向 P1 方向的“长度有多长”。 曲线的参数形式为:
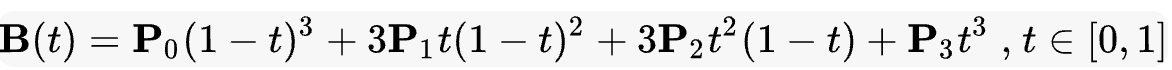
示意图
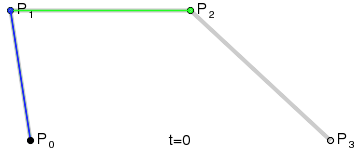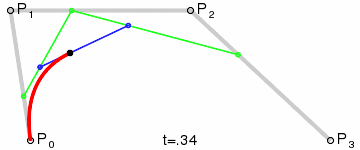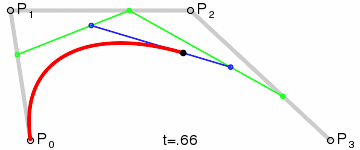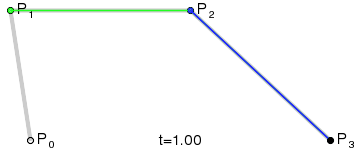
# n 次方贝塞尔曲线
n 阶贝塞尔曲线可如下推断。给定点 P0、P1、…、Pn,其贝塞尔曲线即
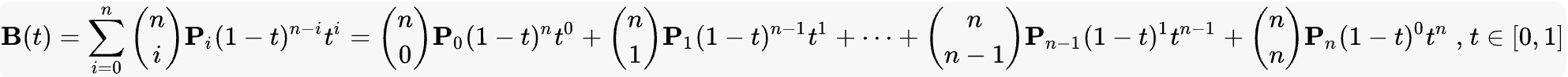
例如 n=5
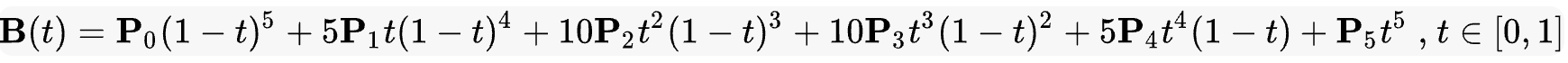
.png)
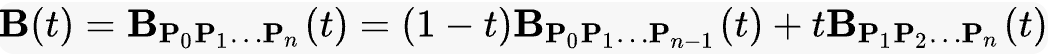
用平常话来说,n 阶的贝塞尔曲线,即双 n−1 阶贝塞尔曲线之间的插值。
# 贝塞尔的升阶和降阶
# 图像证明
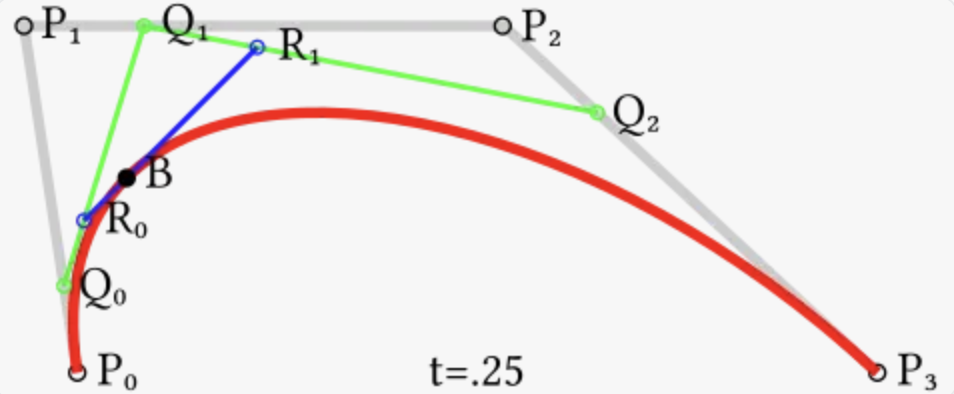
我们还是从三次开始,从图片分析,可以看出来如下规律
- B 由线性(R0,R1),
- R0 由线性(Q0,Q1),R1 由线性(Q1,Q2)
- Q0 由线性(P0,P1),Q1 由线性(P1,P2),Q2 由线性(P2,P3)
来迭代一下上述的公式
- B 由线性(R0,R1),
- R0 由二次( P0,P1,P2),R1 由二次(P1,P2,P3)
最后再迭代一次
- B 由三次(P0,P1,P2,P3)
# 数学证明

展开合并到最后,可以得到我们的证明结果 我们可以发现贝塞尔曲线是可以很方便的升阶和降阶的
这个性质,让三次贝塞尔成了最广泛的应用,二次无法表达 S 曲线,四次及更高的需要更多的控制点,复杂度明显变高
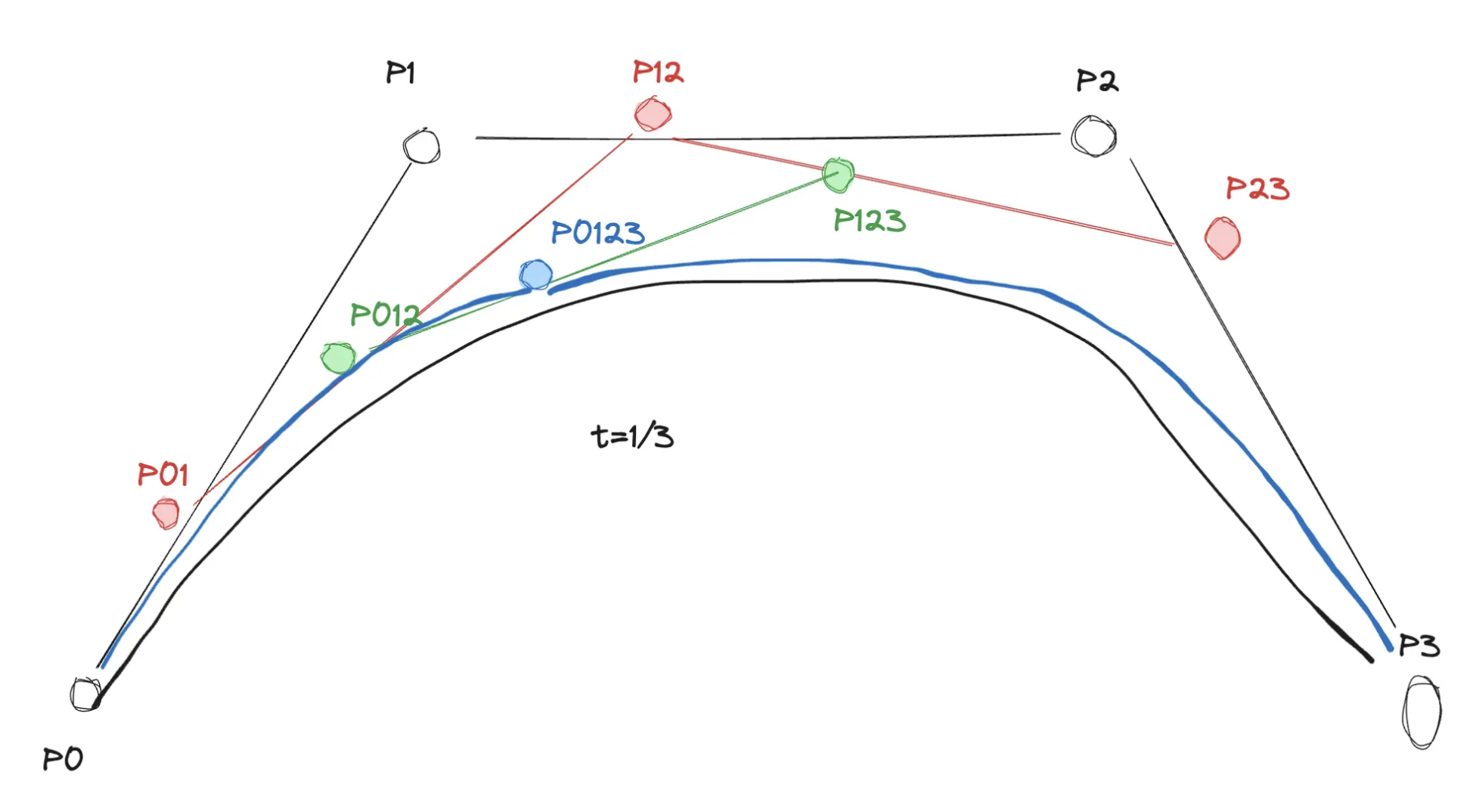
# 贝塞尔的可拆分性
De Casteljau 算法 (opens new window)
function lerp(p0, p1, t) {
return {
x: (1 - t) * p0.x + t * p1.x,
y: (1 - t) * p0.y + t * p1.y,
};
}
function deCasteljauSplit(p0, p1, p2, p3, t) {
const p01 = lerp(p0, p1, t);
const p12 = lerp(p1, p2, t);
const p23 = lerp(p2, p3, t);
const p012 = lerp(p01, p12, t);
const p123 = lerp(p12, p23, t);
const p0123 = lerp(p012, p123, t);
return {
left: [p0, p01, p012, p0123],
right: [p0123, p123, p23, p3],
};
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
通过这个算法我们可以看出来,新构造的两端 B(p0, p01, p012, p0123) 和 B(p0123, p123, p023, p3) 和原来的 B(p0,p1,p2,p3), 在分割点处是连续的(连接) 在分割点导数是一致的(平滑) 在分割点二阶导数是一致的(曲度) 数学证明在这里省略
有了这个性质后,贝塞尔曲线就非常方便的可以进行拆分,转换,存储
# 图形转换
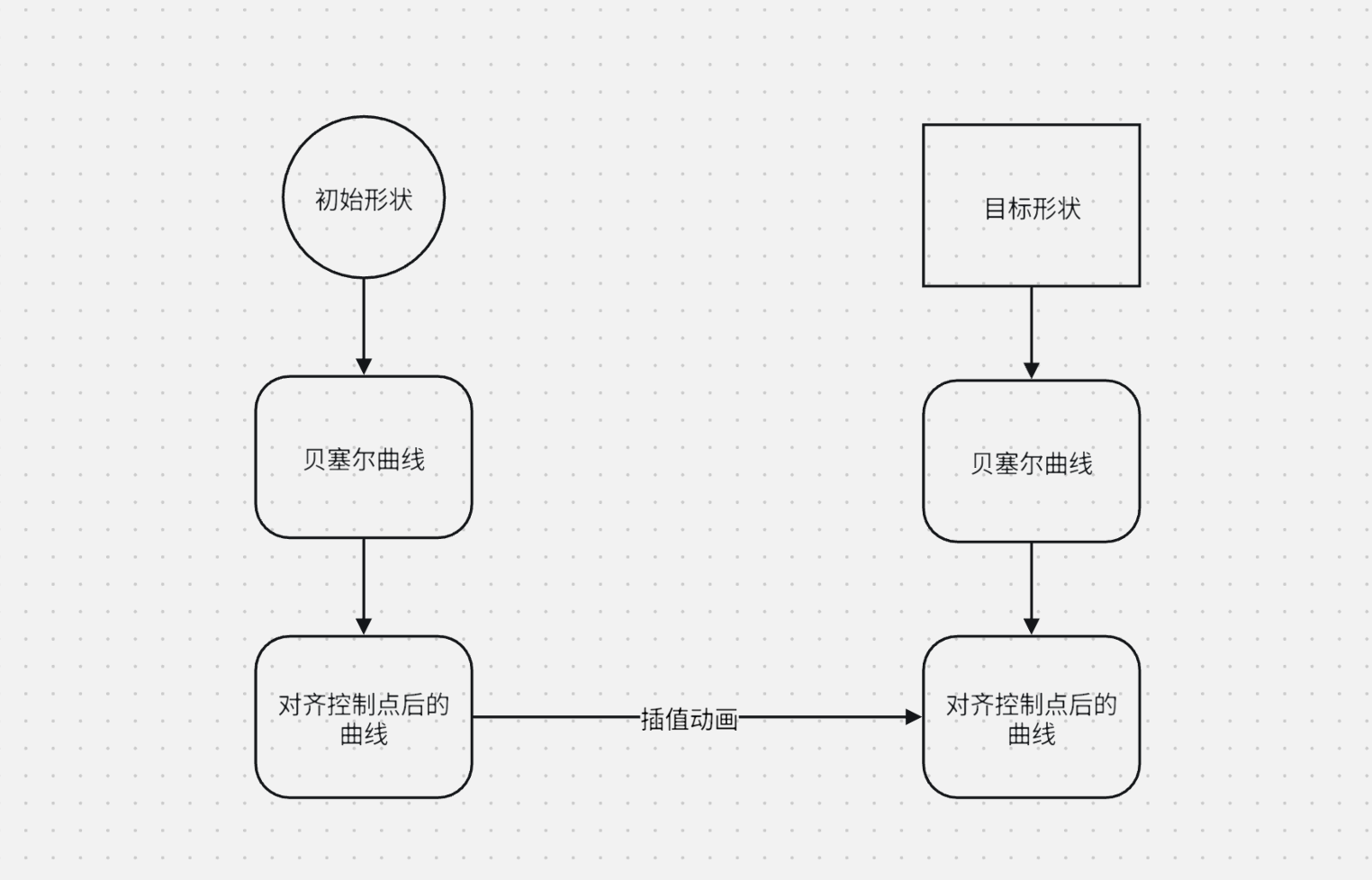
# 圆形转换
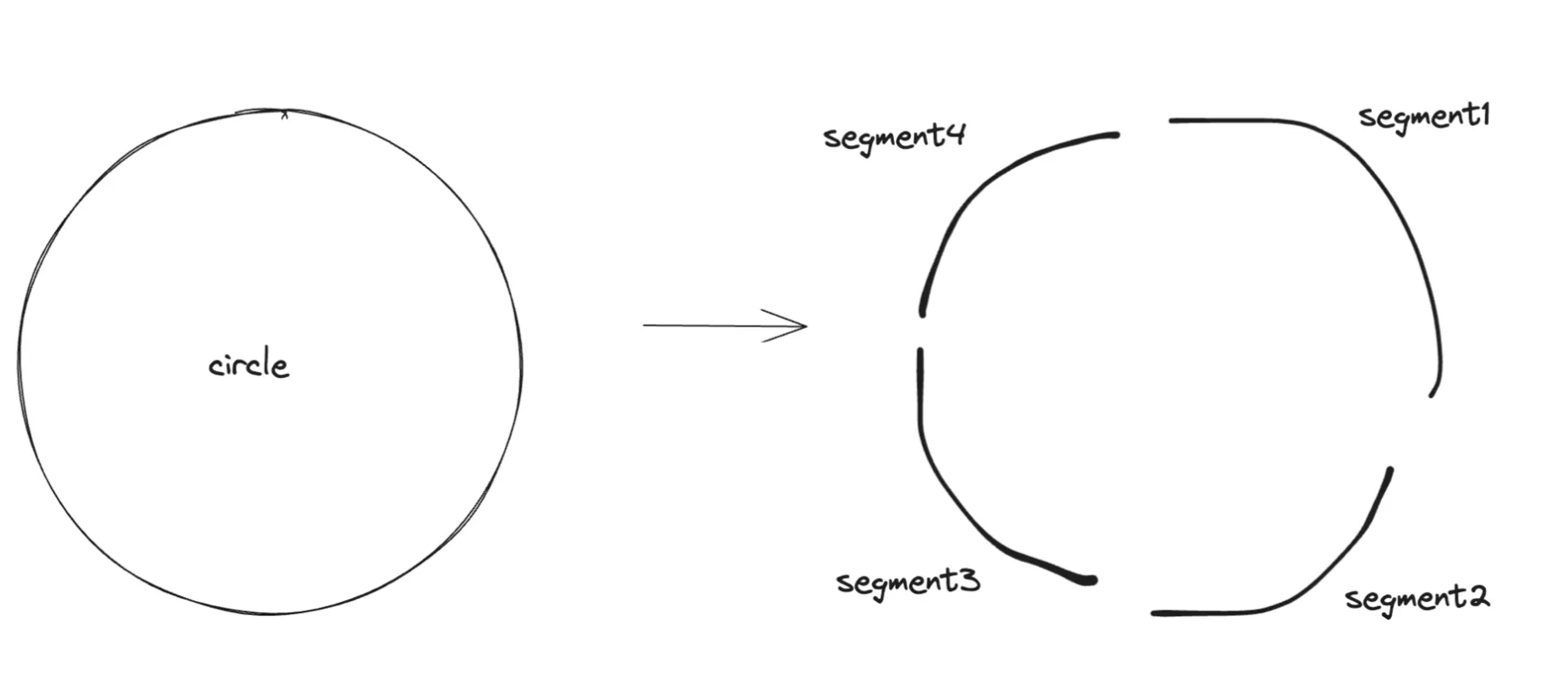
// from top, clockwise rotate
function getBezierCurvesFromCircle(cx, cy, r) {
const k = 0.5522847498;
const offset = k * r;
return [
// start
cx,
cy - r,
// curve 1
cx + offset,
cy - r,
cx + r,
cy - offset,
cx + r,
cy,
// curve2
cx + r,
cy + offset,
cx + offset,
cy + r,
cx,
cy + r,
// curve 3
cx - offset,
cy + r,
cx - r,
cy + offset,
cx - r,
cy,
// curve 4
cx - r,
cy - offset,
cx - offset,
cy - r,
cx,
cy - r,
];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 矩形转换
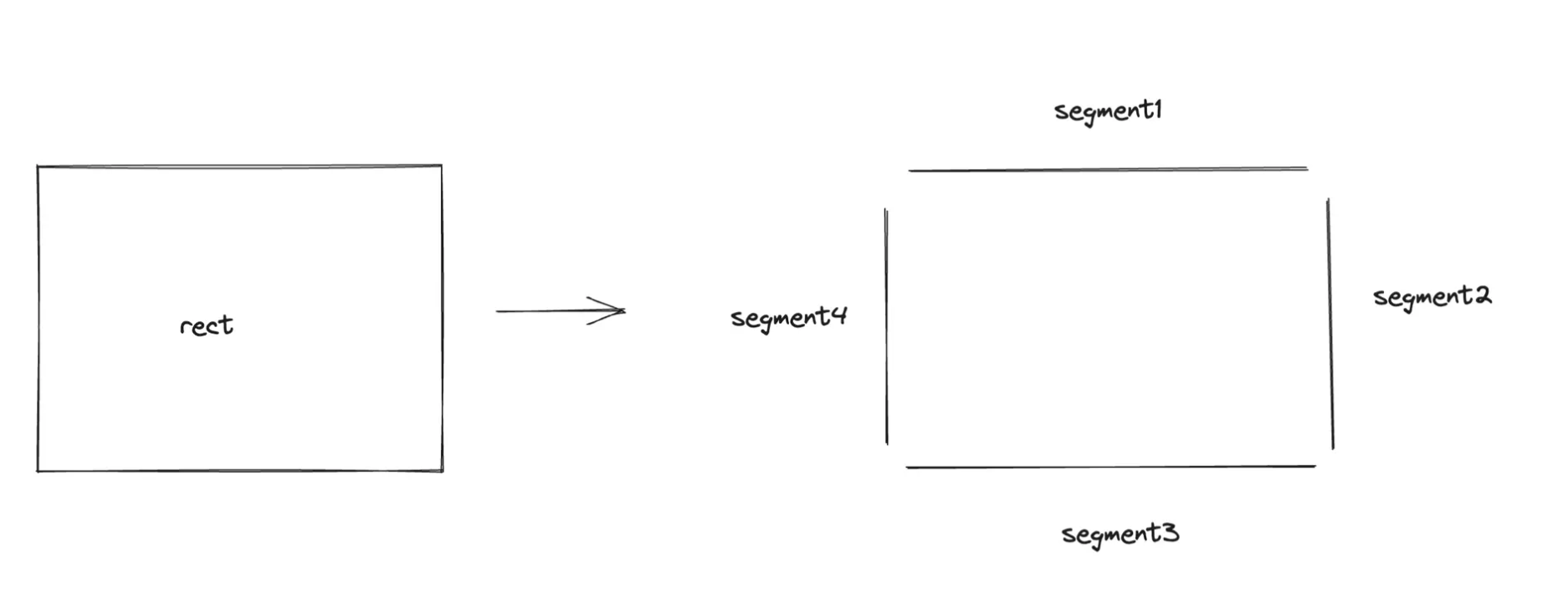
// from left top, clockwise rotate
function getBezierCurvesFromRect(p0, p1, p2, p3) {
const offset = 1 / 4;
const width = p1.x - p0.x;
const height = p2.y - p1.y;
return [
// start
p0.x,
p0.y,
// curve1
p0.x + offset * width,
p0.y,
p1.x - offset * width,
p1.y,
p1.x,
p1.y,
// curve2
p1.x,
p1.y + offset * height,
p2.x,
p2.y - offset * height,
p2.x,
p2.y,
// curve3
p2.x - offset * width,
p2.y,
p3.x + offset * width,
p3.y,
p3.x,
p3.y,
// curve4
p3.x,
p3.y - offset * height,
p0.x,
p0.y + offset * height,
p0.x,
p0.y,
];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 三角转换
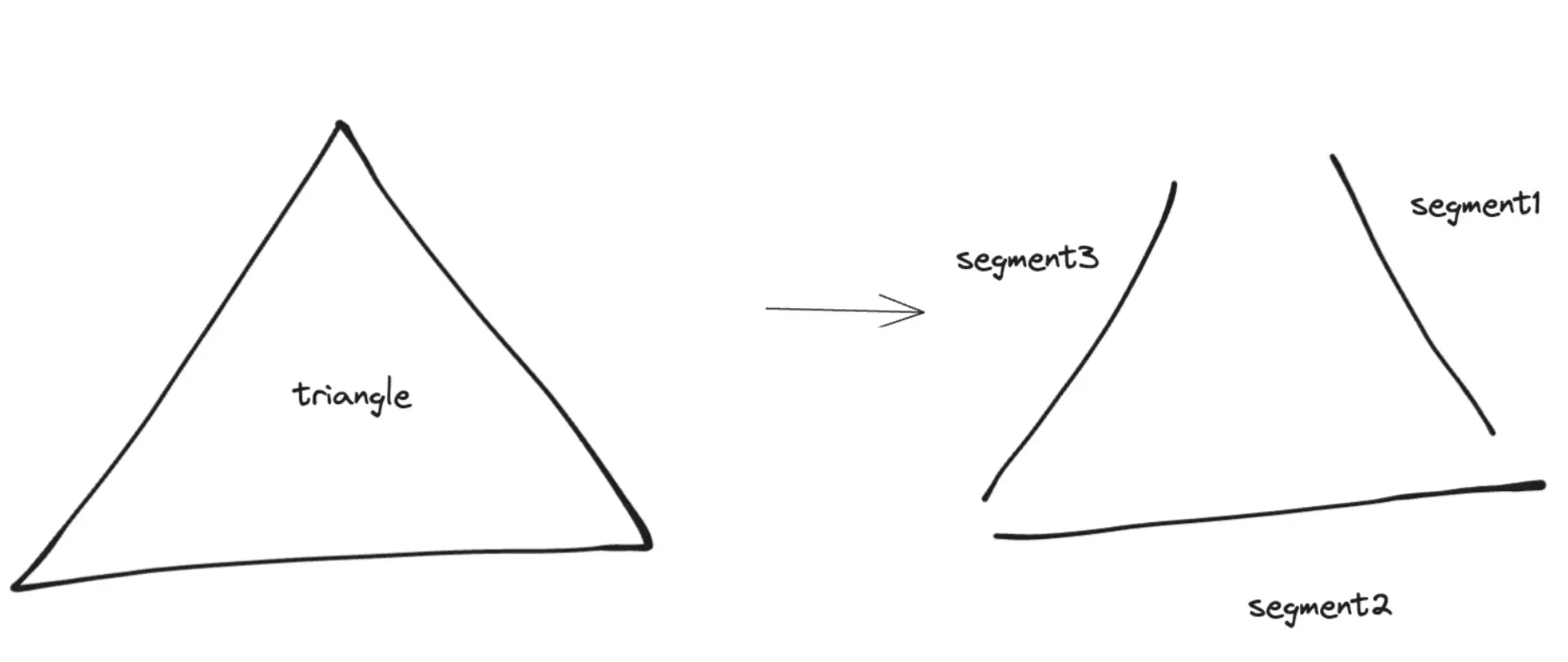
// from top, clockwise rotate
function getBezierCurvesFromTriangle(p0, p1, p2) {
const offset = 1 / 4;
const width = p1.x - p0.x;
const height = p2.y - p1.y;
return [
// start
p0.x,
p0.y,
// curve1
p0.x + offset * (p1.x - p0.x),
p0.y + offset * (p1.y - p0.y),
p1.x - offset * (p1.x - p0.x),
p1.y - offset * (p1.y - p0.y),
p1.x,
p1.y,
// curve2
p1.x + offset * (p2.x - p1.x),
p1.y + offset * (p2.y - p1.y),
p2.x - offset * (p2.x - p1.x),
p2.y - offset * (p2.y - p1.y),
p2.x,
p2.y,
// curve3
p2.x + offset * (p0.x - p2.x),
p2.y + offset * (p0.y - p2.y),
p0.x - offset * (p0.x - p2.x),
p0.y - offset * (p0.y - p2.y),
p0.x,
p0.y,
];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 对齐控制点
对齐有很多种方式,我们拿三角形要对齐矩形来,可以观察到这里是差一条边的,那么我们要对齐的话就大概下面几种方式
# 3 +1
多复制一段重复的
# 2 + 0.5 + 0.5
将某一段拆分为一半
# 3 * 4
求最小公约数,然后三角形没条边分为 4 段,矩形每条边分为 3 段
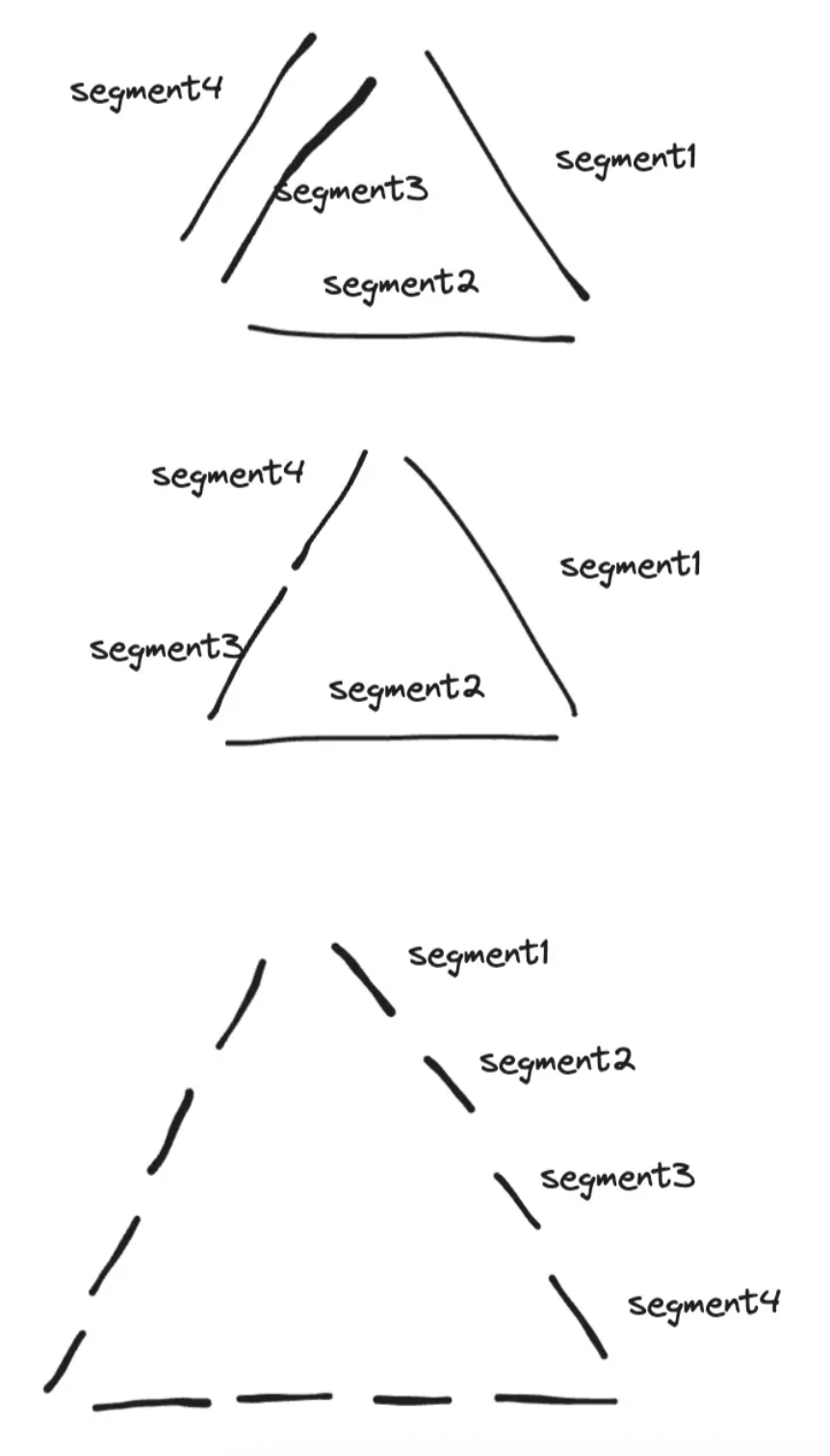
这里展示将第三段分割为二的方式
function lerp(p0, p1, t) {
return {
x: (1 - t) _ p0.x + t _ p1.x,
y: (1 - t) _ p0.y + t _ p1.y,
};
}
// deCasteljauSplit
function splitCurve(p0, p1, p2, p3, t) {
const p01 = lerp(p0, p1, t);
const p12 = lerp(p1, p2, t);
const p23 = lerp(p2, p3, t);
const p012 = lerp(p01, p12, t);
const p123 = lerp(p12, p23, t);
const p0123 = lerp(p012, p123, t);
// return two curve
return {
left: [
// curve1
p0.x,
p0.y,
p01.x,
p01.y,
p012.x,
p012.y,
p0123.x,
p0123.y,
],
right: [
// curve2
p0123.x,
p0123.y,
p123.x,
p123.y,
p23.x,
p23.y,
p3.x,
p3.y,
],
};
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 插值动画
插值动画其实比较简单,我们只需要对初始和目标的贝塞尔曲线的数据进行一一对应来插值就好
drawBezierArr(
data1.map((x, index) => {
return data2[index] _ (1 - t) + data1[index] _ t;
})
);
2
3
4
5
# 一对多/多对一 动画
它的本质其实还是一对一的延伸,我们需要在最开始,将一转为多,这样就可以实现这个酷炫的效果
const rectGroup = splitRect(
{ x: 50, y: 50 },
{ x: 200, y: 50 },
{ x: 200, y: 200 },
{ x: 50, y: 200 },
row,
col
);
const rectGroupData = rectGroup.map(({ p0, p1, p2, p3 }) => {
return getBezierCurvesFromRect(p0, p1, p2, p3);
});
const circleGroup = new Array(col _ row).fill().map((x) => {
return {
cx: 100 + Math.random() _ 300,
cy: 100 + Math.random() \* 300,
r,
};
});
const circleGroupData = circleGroup.map(({ cx, cy, r }) => {
return getBezierCurvesFromCircle(cx, cy, r);
});
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Reference