# 碎语
人间如隙时光如驹
不管怎么说,这是久违的又一次更新。
# 前言
这是一个从准备写到实际开始写拖了一年多的文章。起源是最开始去食堂吃饭,要从地下车库走,然后地下车库的墙上就画着一副大象图。第一次看到的时候就想起了不知道从哪里听到的一句谚语。用四个参数就可以画出一个大象。后面闲暇时候回去查了一下,确实是有一篇关于这个的论文。
Drawing an elephant with four complex parameters (opens new window)
弗里曼·戴森(Freeman Dyson)人生的转折点发生在1953年春季的一次颁奖典礼上,当时恩里科·费米(Enrico Fermi)引用约翰尼·冯·诺依曼(Johnny vonNeumann)的话,批评了戴森模型的复杂性:“我可以用四个参数拟合大象,甚至可以用五个参数使他摆动鼻子。” 从那以后,它成为了物理学家的一句著名的谚语。但是还没有任何人去成功的证明这句话。
为了去参数化一头大象,我们注意到可以把大象轮廓转化成一系列 x(t), y(t) 的点集。随着时间的变化,x,y 点沿着大象轮廓进行变化。如果速度均匀,则 t 可以看作是周长。下面我们把 x(t), y(t) 展开为傅立叶级数的形式
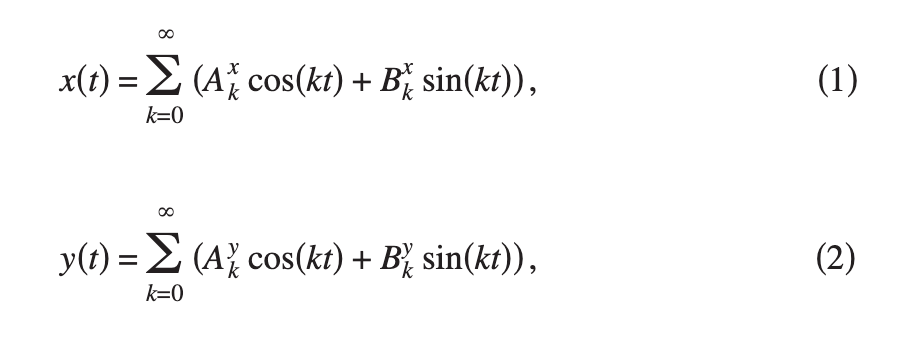
这里 A B 参数为展开的系数,较低的指标 k 代表为当前是傅立叶的第几展开,较高的参数则代表当前是 x 的展开还是 y 的展开
使用这种展开为 xy 坐标系的方式,我们可以通过构造轮廓来分析图像,并且计算出展开式的系数(使用傅立叶分析的标准方法)。通过不断的代入小间距 t,生成的点可以平滑图像,这种方式和用像素点保存图像的方式比,可以大大减少表达一副图像的所需信息。举个例子, Székely et al 用这种方法分割磁共振成像数据。 使用相似的方法分析红细胞的形状,并使用球谐函数展开作为傅立叶坐标展开的3D化
在下面这种情况下,这些傅立叶系数表达了对给定形状的一个最完美的拟合。k=0 时对应于形状的质心。k=1 时对应于最好的椭圆拟合。随着 k 的提高,可以不断的修改最终图像的美观性,达到完全拟合。通过把这些系数结合到复数中,我们可以得到4组复数参数,来等效拟合大象图像。第五个参数的实数参数代表为一个摇晃参数,它用来代表鼻子连接到身体的 y 【论文这里是 x ,但是实际使用下来应该对应的是 y】值,其虚数部分代表大象眼睛。所有的参数都在表中有表示出来。

最后产生的图像比较简单卡通,但是仍然可以看出来它是一个大象,尽管使用傅立叶来构建图像不是一个新使用,但是我们也清楚地证明了其在减少描述二维轮廓所需的参数数量方面的有用性。在参考资料5中,我们可以找到它的可视化工具
现在我们使用这个工具,用我们得到的四个参数开始来拟合大象。图b
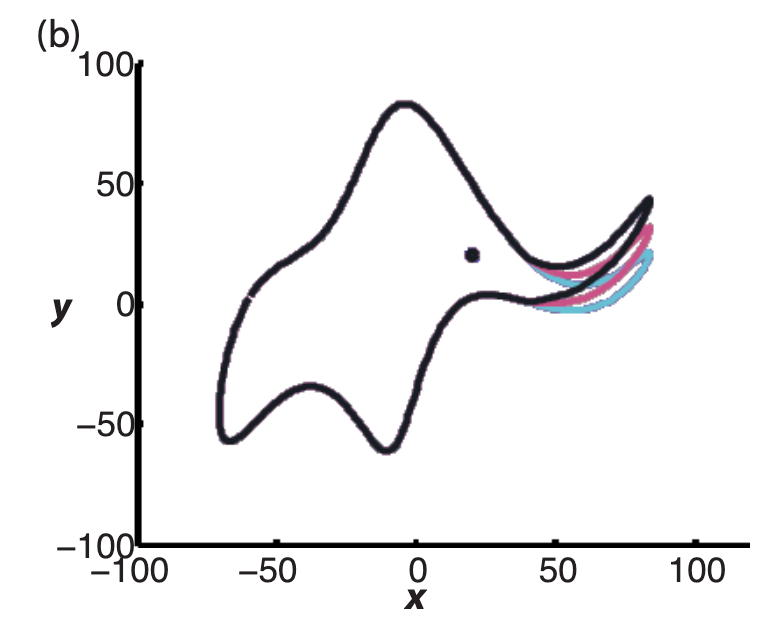
在 1975 年,同样有人用了 30 个系数来描述出了下图a
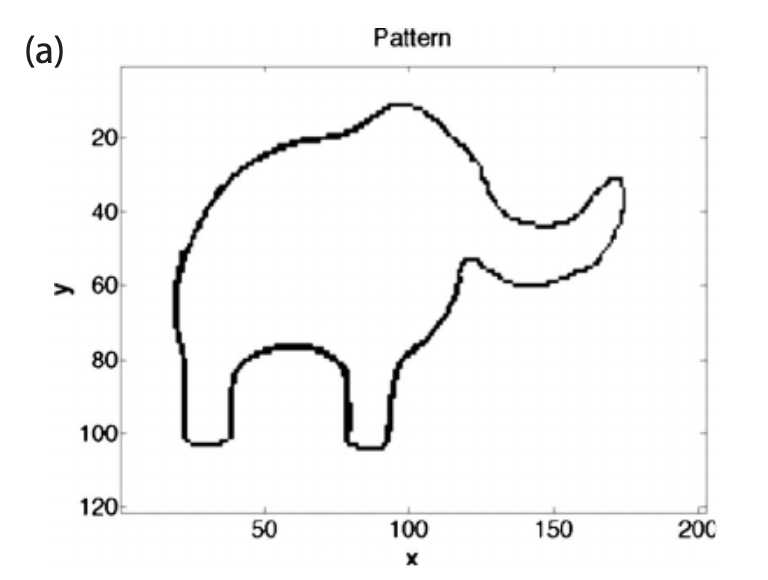
通过消除幅度小于最大幅度的10%的分量,我们获得了一个近似频谱。通过不断消减构造,可以把它最终表达为4个复数系数,同时也证明了谚语的正确性。【我可以用四个参数拟合大象,甚至可以用五个参数使他摆动鼻子。】
# 原理
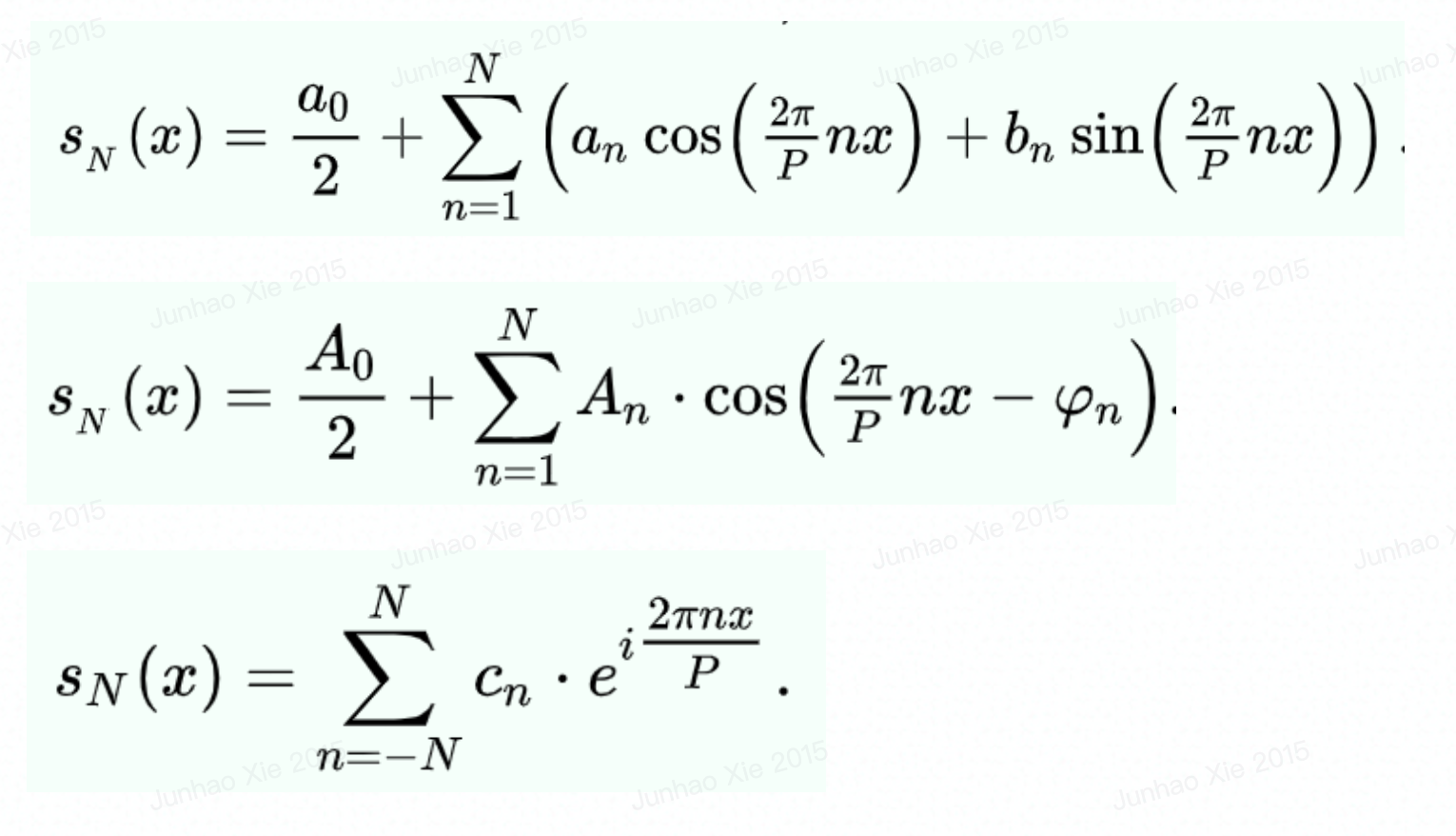
在数学中,傅里叶级数是把类似波的函数表示成简单正弦波的方式。更正式地说,对于满足狄利克雷定理的周期函数,其傅里叶级数是由一组简单振荡函数(正弦与余弦函数,或等价的复指数函数)的加权和表示的方法。离散时间傅里叶变换是一个周期函数,通常用定义傅里叶级数的项进行定义。另一个应用的例子是Z变换,将傅里叶级数简化为特殊情形 |z|=1。傅里叶级数也是采样定理原始证明的核心。
举个🌰,方波
方波的数学形式 (opens new window) 一个题外话,方波中存在一个固定的冲量,吉布斯现象 (opens new window)
# 代码验证
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>Document</title>
</head>
<body>
<p></p>
<canvas id="canvas" width="200" height="200"></canvas>
<script>
var canvas = document.getElementById("canvas"),
ctx = canvas.getContext("2d");
var elephant = [];
var π = Math.PI;
var τ = 2 * Math.PI;
var P = 360;
var theta = 0;
var width = 200;
var height = 200;
var scale = 1;
FourierCoefficient = function (real, imag) {
this.real = real;
this.imag = imag;
};
// p1 = 50 - 30j
// p2 = 18 + 8j
// p3 = 12 - 10j
// p4 = -14 - 60j
// p5 = 40 + 20j
// x(t): [ 0.+50.j , 0.+18.j , 12. +0.j , 0. +0.j , -14. +0.j]
// y(t): [ -60.-30.j , 0. +8.j , -0.-10.j , 0. +0.j , 0. +0.j]
var P1 = new FourierCoefficient(50, -30);
var P2 = new FourierCoefficient(18, 8);
var P3 = new FourierCoefficient(12, -10);
var P4 = new FourierCoefficient(-14, -60);
var P5 = new FourierCoefficient(40, 20);
Point = function (x, y) {
this.x = x;
this.y = y;
this.radius = 3;
};
function makeElephant() {
var x, y;
for (var i = 0; i < P; i++) {
var t = τ * (i / P);
x =
// cos
P4.imag * Math.cos(1 * t) +
0 * Math.cos(2 * t) +
0 * Math.cos(3 * t) +
0 * Math.cos(4 * t) +
// sin
P1.imag * Math.sin(1 * t) +
P2.imag * Math.sin(2 * t) +
P3.imag * Math.sin(3 * t) +
0 * Math.sin(4 * t);
y =
// cos
0 * Math.cos(1 * t) +
0 * Math.cos(2 * t) +
P3.real * Math.cos(3 * t) +
0 * Math.cos(4 * t) +
P4.real * Math.cos(5 * t) +
// sin
P1.real * Math.sin(1 * t) +
P2.real * Math.sin(2 * t) +
0 * Math.sin(3 * t) +
0 * Math.sin(4 * t);
elephant.push(new Point(x, y));
}
}
function draw() {
ctx.translate(width / 2, height / 2);
ctx.scale(scale, scale);
ctx.strokeStyle = "steelblue";
let delta = (Math.cos(τ * theta) - 0.5) / 10;
// eye
ctx.arc(P5.imag, -P5.imag, 4, 0, τ);
ctx.fill();
elephant.forEach((p, index) => {
ctx.beginPath();
let _p = Object.assign({}, p);
// 这里根据 delta 做一个动画
if (_p.x > P5.real) {
_p.y += (_p.x - P5.real) * delta;
}
// body
ctx.arc(_p.x, _p.y, _p.radius, 0, τ);
ctx.stroke();
});
ctx.setTransform(1, 0, 0, 1, 0, 0);
}
makeElephant();
function loop() {
ctx.clearRect(0, 0, width, height);
theta += 0.1;
draw();
setTimeout(() => {
loop();
}, 200);
}
loop();
</script>
</body>
</html>
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
# 参考
https://www.youtube.com/watch?v=r6sGWTCMz2k
https://www.jezzamon.com/fourier/zh-cn.html
https://alexmiller.phd/posts/fourier-series-spinning-circles-visualization/