凸包问题 (opens new window)

在给定的点中，找出有限点构造一个最小凹边形，使其可以将给定的所有点都包含在内

咕咕咕，拖了两个月 hhhh，本来这个是偶然在群里看到有人想做一个可视化的凸包问题输出。于是研究了一下。

思路解析

对于我这么一个从来没做过相关图算法的来说，上来会很没有头脑。唯一能想到的只有一个大概思路 判断点是否在线段的某一边，因为凸包的性质，那么对于给定的所有点，这些点必定在凸包边线段的一侧或者其上。

判断点是否在线段的某一边

那么如何判断呢？这里要引入一个数学概率，叉乘 (opens new window)

由叉乘的定义可知，在三维坐标系中。向量 a 叉乘 向量 b 可以得到一个垂直于 a b 向量组成平面的新向量 c，且它的模长等于向量 a b 形成的平行四边形面积。且 c 根据 a b 的方向不同，也会有自己的方向。这里可以根据右手定则 (opens new window)来得知向量 c 的方向。

那么在这里，我们不需要用到全部 叉乘 的特点。由于我们凸包构造的是二维坐标系，那么扩展到三维的话 z 向量系数一定为 0。所以简单来说二维平面上三点 A, B, C 构造出的向量 ab 叉乘 ac 得出的向量必定是在 z 轴上的向量(0x, 0y, kz)。那么通过计算出单位向量 z 的系数 k。 如果 k > 0 ，那么点 C 在向量 ab 的左边。 k = 0， 点 C 在向量 ab 上。 k < 0，点 C 在向量 ab 右边。

叉乘的计算可以写为

所以如果在二维坐标系中，就可以简化为 U ✖️ V = (u1v2 - u2v1)k

这里把 u v 更换为 x y， 那么我们可以根据 (x1y2 - x2y1) 的值是否大于等于 0 来进行判断

然后以它为核心思想，从最基础的穷举方法来开始优化

给定 n 个点，那么会有 n * (n - 1) / 2 条线，对每一条线进行计算，剩余的 (n - 2) 个点是否都位于这点线段的一侧。如果是，那么这两点为 凸点。

穷举法复杂度为 O(n^3)

这里可以继续对穷举法进行优化，首先取纵坐标最小的一个点，如果有两个就取其中一个，它肯定在凸包上。

然后以它为极坐标中心，对剩下的所有点进行一个角度排序，排序结果如下图。

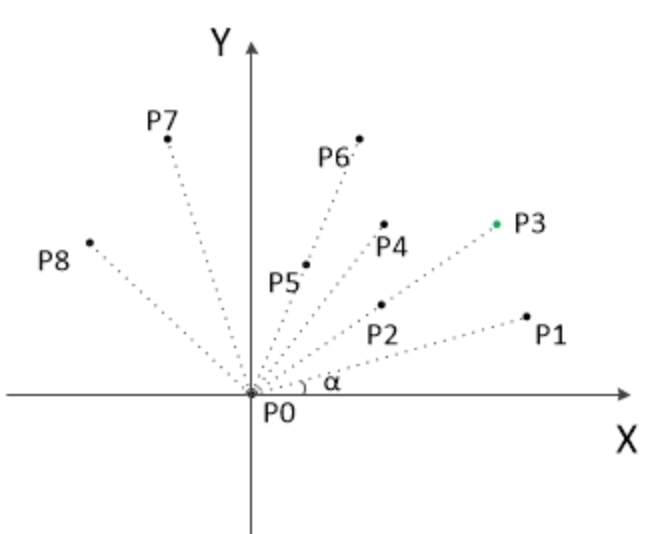
然后就按顺序依次对每一个点 $P_k$ 开始依次尝试剩下的 $P_{n-k}$ 个点，找到第一个满足条件的点【其他点都在$P_kP_{n-k}$线段左侧】。

这样可以降低复杂度到 O(n^2)

到了这一步，想继续优化就得换一个思路，考虑是否可以不再对每一个点都进行尝试。Graham (opens new window)

这里通过从最低点开始，然后分析凸包的特点找规律，距离它角度最小的第一个点肯定是凸包上的点【当然角度最大的也是】，那么把 p0p1 入栈，接着考虑在线段 p1p2 是否是左转【可以想象一个人先沿着 p0p1 走，到了 p1 的时候是需要向左转还是向右转】。如果是向左，那么这个点入栈，继续下一个点。如果这个点向右，那么说明当前栈顶不是凸包上的点，出栈。然后再次拿栈顶两点来和当前拿的点比较。这样如此反复

复杂度 O(n * log n)

最后附上 Graham 的实现

// 叉乘
function crossProduct(p0, p1, p2) {
  const vectorA = {
    x: p1.x - p0.x,
    y: p1.y - p0.y,
  }
  const vectorB = {
    x: p2.x - p0.x,
    y: p2.y - p0.y,
  }
  // 向量叉乘，这里简化了 z 轴
  return vectorA.x * vectorB.y - vectorA.y * vectorB.x
}

function getConvexHull(pointData) {
  const result = []
  const arr = pointData.sort((a, b) => a.y - b.y)
  const p0 = arr.shift()

  // 最低点一定在凸包上，有多个最低点可以随便选一个
  result.push(p0)

  // 按角度排序
  const sortedPoint = arr
    .map((p) => {
      const cos = (p.x - p0.x) / Math.sqrt(Math.pow(p.y - p0.y, 2) + Math.pow(p.x - p0.x, 2))
      return {
        ...p,
        cos,
      }
    })
    .sort((a, b) => b.cos - a.cos)
    .map((p) => {
      return { x: p.x, y: p.y }
    })

  // 按照凸包的性质，第一个点必定在凸包上
  result.push(sortedPoint.shift())

  sortedPoint.forEach((p, index) => {
    while (crossProduct(result[result.length - 2], result[result.length - 1], p) < 0) {
      // 在右方，说明栈顶不是凸包上的点
      result.pop()
    }
    // 在一条线上的情况，多去一个点，属于优化操作
    if (crossProduct(result[result.length - 2], result[result.length - 1], p) === 0) result.pop()

    // 在左边及线上
    result.push(p)
  })

  return result
}

const pointData = [
  { x: 1, y: 28 },
  { x: 2, y: 1 },
  { x: 4, y: 1 },
  { x: 5, y: 11 },
  { x: 6, y: 21 },
  { x: 7, y: 43 },
  { x: 10, y: 115 },
]
const areaData = getConvexHull(JSON.parse(JSON.stringify(pointData)))

/*
 * console areaData:
 *
 *{x: 2, y: 1}
 *{x: 4, y: 1}
 *{x: 6, y: 21}
 *{x: 7, y: 43}
 *{x: 10, y: 115}
 *{x: 1, y: 28}
 */